5.12 Atoms (Discrete Energy Levels, Transitions, and Statistical Constraints)

Home ／ Chapter 5: Microscopic Particles

I. Intro and Aims

This section explains three core ideas in plain language:

• Discrete energy levels: why electrons in an atom “stay” only in a few allowed shells and shapes rather than any energy.
• Transitions and spectra: how electrons move between levels and settle the energy “accounts” as light, and why spectral lines are discrete with different strengths.
• Statistical constraints: what “single occupancy” and “paired occupancy” mean, why “no double-occupancy in the same state,” Hund’s rules, and how these acquire a material picture in Energy Filament Theory (EFT).

We avoid heavy formulas and use familiar analogies—such as classrooms and seats or probability clouds—when helpful. Inline symbols like n, l, m, ΔE, and Δl serve only as labels.

II. Textbook Baseline (For Comparison)

• The atomic nucleus provides a Coulomb potential. Electrons occupy quantum states that satisfy boundary and symmetry conditions.
• Allowed states are labeled by the principal quantum number n, orbital angular momentum l, magnetic quantum number m, and spin; s/p/d/f correspond to l = 0/1/2/3.
• Electrons in the same atom follow Fermi–Dirac statistics and the Pauli exclusion principle: each quantum state holds at most two electrons with opposite spins.
• Transitions follow selection rules (typically Δl = ±1). The energy difference ΔE enters or leaves as a photon, producing discrete spectral lines; line strengths follow from transition matrix elements; linewidths reflect natural lifetime, Doppler and collisional effects, and external fields.

These are successful, experimentally tested frameworks. On this basis, we offer a unified, material intuition in Energy Filament Theory (EFT).

III. Core Picture in Energy Filament Theory: A Shallow Tension Basin and Closed-Filament Standing-Phase Channels

1. The energy sea: Treat the vacuum as a medium with properties. Its locally variable “tightness” defines a tension that sets limits on propagation and a local scale for drag and guidance.
2. Shallow tension basin: The nucleus “presses” a near-spherically symmetric shallow basin into this sea. From afar it looks like mass and guidance; up close it provides the “terrain boundary” for stable electron states.
3. Electron as a closed filament ring: An electron is not a point but a self-sustained, closed loop of energy filament. To persist without dispersing, it must lock its internal phase cadence to standing-phase channels shaped by the surrounding tension terrain.
4. Standing-phase channels = allowed energies and shapes:
   • s channels: roughly spherical “ring-belt probability clouds.”
   • p channels: three mutually orthogonal “dumbbell-like probability clouds.”
   • Higher d/f channels: more intricate oriented geometries.
5. Intuition: Discrete levels are the channels in which a filament can close its phase and minimize energy within the basin. There are only a few such channels, so the spectrum is discrete.

IV. Why Energy Levels Are Discrete (An EFT Intuition)

• Boundaries and economy: To be self-sustained, the filament balances its internal cadence with the basin’s restoring pull, forming a stable loop. Only a small set of geometry–cadence combinations manages to both close and save energy—these map to the discrete “addresses” labeled by n, l, and m.
• Shapes selected by terrain: A near-spherical basin favors s. When angular momentum must be carried, geometry “grows” two-lobed p forms; above that come d/f. Shapes are not just labels; they result from a three-way compromise among terrain, phase closure, and energy cost.
• Hierarchy: Outer channels have larger extent and looser constraints but are easier to disrupt. This gives an intuitive reason why highly excited states (large n) ionize more readily.

V. Statistical Constraints: Single Occupancy, Paired Occupancy, and “No Two in One”

1. A material view of exclusion (Pauli):
2. If two filament loops share a channel with exactly the same phase, their near-field tension shears conflict, energy cost spikes, and the structure cannot sustain itself. Two resolutions exist:
   • Disperse into different channels (favoring single occupancy first).
   • Phase complement within the same channel (opposite spin pairing), letting two electrons share one probability cloud without fatal shear—this is paired occupancy.
3. Empty, single, and paired:
   • Empty: no filament resides in that channel.
   • Single: one filament alone—most stable.
   • Paired: two filaments with complementary phase co-reside; stable but slightly higher energy than two separate singles.
4. Hund’s rule, materially:
5. In a triply degenerate set (e.g., pₓ/pᵧ/p𝓏), filaments spread out to single-occupy different orientations first, distributing near-field shear and lowering total energy. Only when forced do they pair up in one orientation. Thus the abstract rules—“two per state max,” “fill singly before pairing”—emerge from concrete thresholds in tension shear and phase complementarity.

VI. Transitions: How Electrons “Settle the Account” as Light

1. Triggers: External input (heating, collisions, optical pumping) or internal redistribution can lift a filament from a low-energy channel to a higher one; excited channels are short-lived and relax to more economical channels after a dwell time.
2. Where the energy goes: Changing channels creates a surplus or deficit that leaves or enters as a packet of disturbances in the energy sea; macroscopically, this is light.
   • Emission: high → low, releasing a disturbance packet (an emission line).
   • Absorption: low → high, absorbing a packet that matches the channel gap (an absorption line).
3. Why lines are discrete: Allowed channels are discrete, so ΔE can take only those differences. Frequencies land in only a few slots.
4. Selection-rule intuition: Channel-to-channel motion must match shapes and handedness and balance angular-momentum and orientation accounts with the sea:
   • The common Δl = ±1 reflects the need to “flip the cloud’s level of shape” to keep energy–angular-momentum–coupling efficiency in balance.
   • Patterns in Δm follow the coupling geometry to external orientation fields (e.g., applied fields or polarization).
5. What sets line strength: Two scales matter—the “phase-overlap area” between channels and the “coupling drag”:
   • Greater overlap and smaller drag → stronger oscillator strength and brighter lines.
   • Poor overlap and large drag → forbidden or weak transitions, producing faint or absent lines.

VII. Line Shapes and Environments: Why One Line Broadens, Shifts, or Splits

• Natural width: Finite dwell time in excited channels gives each channel an intrinsic “window,” i.e., natural broadening.
• Thermal motion (Doppler): Motion of the whole atom nudges the emitted packet’s frequency, which accumulates into Gaussian broadening.
• Collisions (pressure broadening): Repeated “squeeze–release” by neighbors jitters the channel’s phase and widens the profile.
• External fields (Stark/Zeeman): Orientation fields reshape the edges of standing-phase channels and gently pry apart degeneracies, yielding predictable splitting and shifts.
• EFT in one line: A line profile equals a channel’s own window plus its “jitter–rescaling–splitting” inside the surrounding tension and orientation fields.

VIII. Why Higher Environmental Tension → Slower Internal Oscillation → Lower Emission Frequency

• What “Higher Tension” Means, and Two Different Quantities
• a) Setting. Higher environmental tension means the shallow basin sits in a stiffer environment—stronger gravitational potential, higher compression or density, or a strong orientation field—so the Energy Sea is pulled tighter.
• b) Two quantities. The propagation ceiling is the fastest response the medium can support; the standing-phase frequency is the cadence of a bound mode under environmental loading.
• c) Not the same thing. The ceiling can rise even while a bound oscillator slows, because environmental loading drags the oscillator.
• Three Compounded Effects in Energy Filament Theory (EFT)
• a) Deeper/Wider Basin → Longer Loop (Geometric Delay). Raising tension deepens and widens the basin, pushing equal-phase surfaces outward; each beat must traverse a longer closed path, so one lap takes longer.
• b) More Medium Entrained → Higher Effective Inertia (Reactive Loading). Stronger near-field coupling makes each phase turn drag a thicker layer of medium; that carried-along layer acts like added mass and slows the natural cadence. (A spring–mass system vibrates more slowly when immersed in a “thicker” medium.)
• c) Echo Recoupling → Phase Retardation (Nonlocal Delay). Near-field perturbations echo within the basin and feed back, adding a phase “after-ring” to each beat; equivalently, more reactive energy is stored and retrieved per cycle.
• Net Result
• a) The intrinsic bound-mode frequency shifts downward for the same atom and the same channel.
• b) Level spacings shrink, often by an approximately common scale factor.
• c) Therefore adjacent-level ΔE decreases, and spectral lines shift to lower frequencies (a redward move).
• Clarifications
• a) “Doesn’t higher tension speed propagation?” For free waves, the ceiling can rise; a bound oscillator, however, is governed by geometry + added mass + echo delay, which dominate and slow it.
• b) “Is this gravitational redshift?” In EFT, higher gravitational potential corresponds to higher tension; the local atomic “clock” slows via the three mechanisms above. Observed reddening matches general-relativistic redshift, while EFT provides a material coupling-and-geometry route to the same outcome.
• c) Ceiling vs. cadence. A faster free-wave limit does not guarantee a faster bound-mode cadence; loading and delay terms set the beat.
• Intuitive, Testable Leads
• a) Same nucleus, different environments. Near white-dwarf surfaces, atomic lines appear redder than in the lab; in laboratory settings, raising pressure/density/orientation yields repeatable millishifts to the red after standard Stark/Zeeman and pressure-broadening corrections.
• b) Isotopes or isostructural systems. The more easily entrained (higher polarizability, “softer” near field) a system is, the larger the center-frequency drop under the same environmental tension.

IX. Why Electrons Look Cloud-Like and Seem to “Wander”

In EFT, an electron is a closed energy-filament loop, not a tiny ball orbiting the nucleus. It persists only within a few standing-phase channels sculpted by the nucleus’s shallow-tension basin. The observed “cloud” is the appearance probability inside those channels. Forcing the electron into a very narrow region drives near-field tension-shear conflicts; meanwhile momentum (direction and magnitude) must spread to maintain phase closure, which is energetically costly. Stable solutions therefore have finite width, the physical basis of uncertainty.

In addition, the Energy Sea carries Tension Background Noise (TBN) that gently and persistently perturbs the filament’s phase cadence, producing a fine-grained phase walk inside the channel. Beyond the channel’s edge, phase closure fails and destructive self-interference suppresses the amplitude, leaving a dense–faint texture in the cloud. A measurement that localizes the electron briefly tightens the near field; afterward the system relaxes back to an allowed standing-phase pattern. Statistically, the electron behaves like a cloud “wandering” within the permitted region—a steady distribution selected by filament + Energy Sea + boundary conditions, with the “wandering” driven by standing-phase constraints and ever-present background perturbations.

X. Summary

• Discrete energy levels: the few standing-phase channels in a nucleus’s shallow-tension basin where a filament can close phase while minimizing energy.
• Statistical constraints: double occupancy fails when in-phase shear exceeds a threshold; paired occupancy works via phase complementarity; Hund’s rules follow “spread first, pair later” to minimize total shear.
• Transitions and spectra: changing channels settles energy as disturbance packets → discrete spectral lines; strengths are set by cloud overlap and coupling drag.
• Environment → slower cadence → lower frequency: deeper/wider loops (geometric delay) + added mass (reactive loading) + echo delay (nonlocal) act together to lower bound-mode frequencies and shrink spacings, shifting lines redward—consistent with gravitational redshift and grounded in a material picture.

Four Typical Atoms (with Electrons) — Schematic

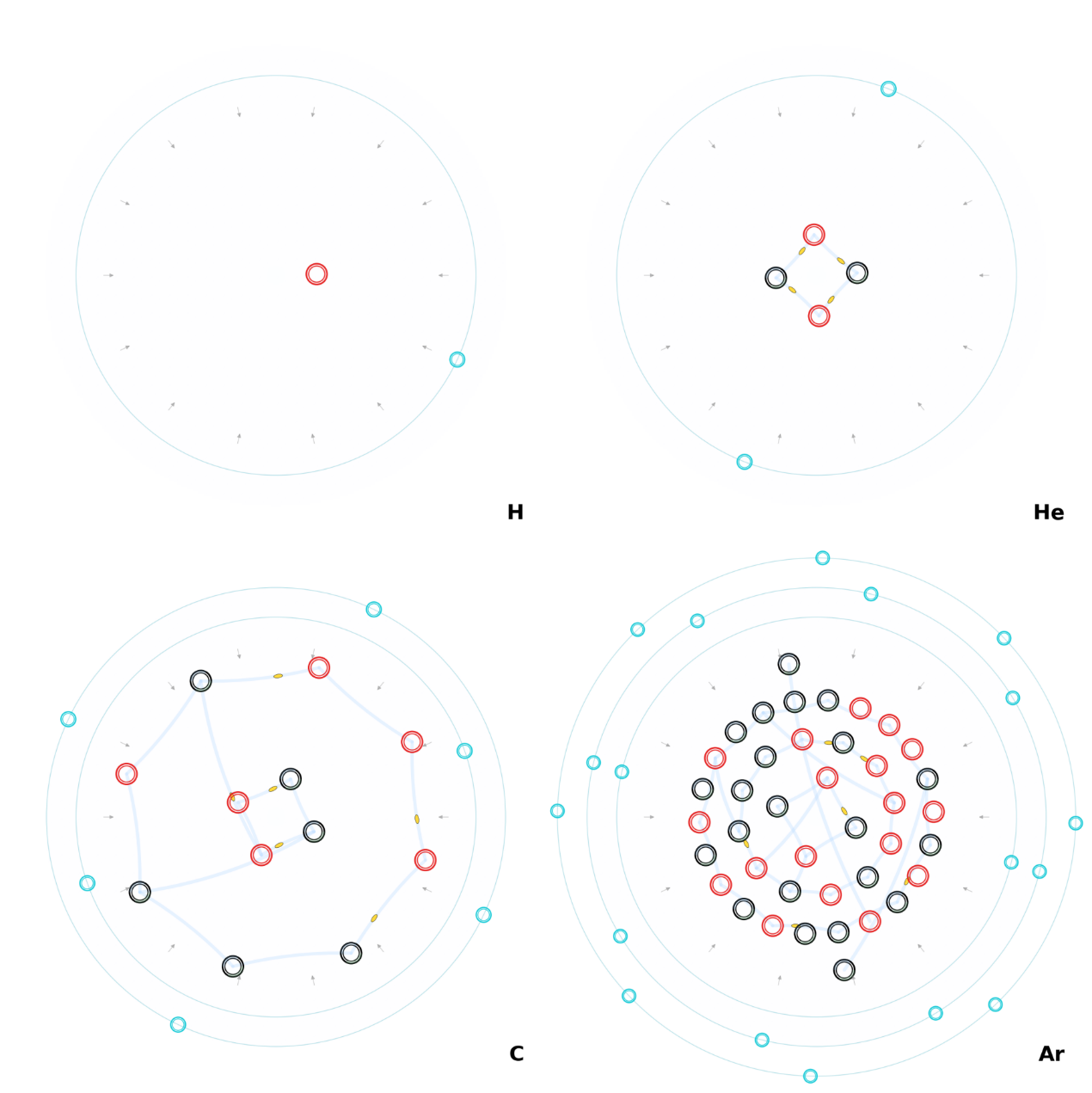
• Nucleons: red rings = protons; black rings = neutrons.
• Color-filament tubes: translucent blue “bands” connecting nucleons (cross-nucleon tension-binding bands); small yellow ellipses depict gluon-like appearances.
• Electrons: cyan mini-loops distributed on discrete electron shells (pale-cyan concentric circles).
• Labels: the element’s English abbreviation (e.g., H, He, C, Ar) appears at bottom-right in white.
• Isotopes and shells: use typical isotopes (H-1, He-4, C-12, Ar-40). Show shell aggregation by principal shells [2, 8, 18, 32] (e.g., Ar = [2, 8, 8]).